Documentation > Tutorials
This example presents how to explore a NetLogo model step by step with an Evolutionary/Genetic Algorithm (EA/GA) in OpenMOLE.
For more generic details regarding the use of Genetic Algorithms within OpenMOLE, you can check the GA section of the methods documentation
In this project, a colony of ants forages for food. Though each ant follows a set of simple rules, the colony as a whole acts in a sophisticated way. When an ant finds a piece of food, it carries the food back to the nest, dropping a chemical as it moves. When other ants "sniff" the chemical, they follow the chemical toward the food. As more ants carry food to the nest, they reinforce the chemical trail.
A visual representation of this model looks like: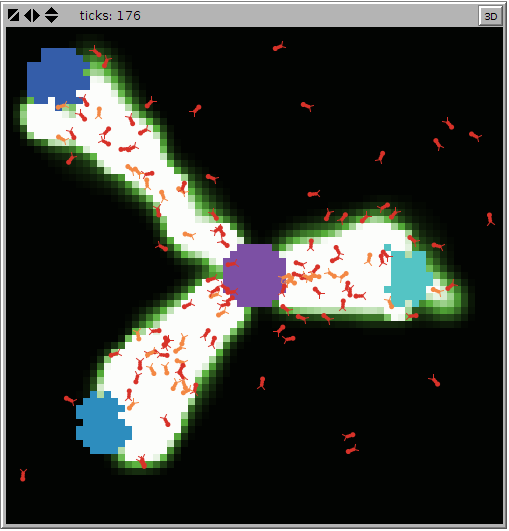 In this tutorial we use a headless version (see NetLogo task documentation) of the model.
This modified version is available here.
In this tutorial we use a headless version (see NetLogo task documentation) of the model.
This modified version is available here.
Ants forage from three sources of food (see the number in the picture below). Each source is positioned at different distances from the Ant colony.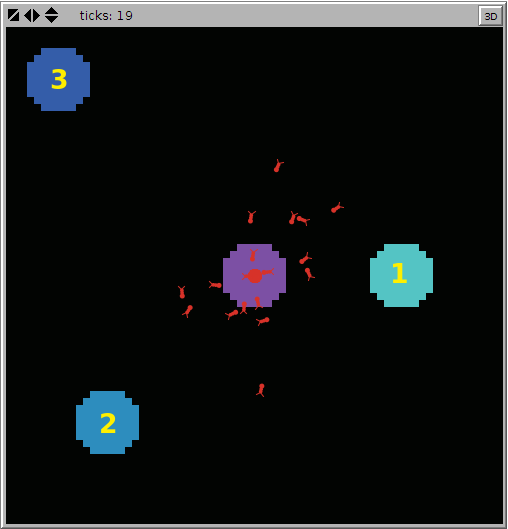 It can be interesting to search for the best combination of the two parameters
It can be interesting to search for the best combination of the two parameters
Notice how the
Content:
The ant model 🔗
In this tutorial we will be using the Ants foraging model, present in the Netlogo library. This model was created by Ury Wilensky. According to NetLogo's website, this model is described as:In this project, a colony of ants forages for food. Though each ant follows a set of simple rules, the colony as a whole acts in a sophisticated way. When an ant finds a piece of food, it carries the food back to the nest, dropping a chemical as it moves. When other ants "sniff" the chemical, they follow the chemical toward the food. As more ants carry food to the nest, they reinforce the chemical trail.
A visual representation of this model looks like:
 In this tutorial we use a headless version (see NetLogo task documentation) of the model.
This modified version is available here.
In this tutorial we use a headless version (see NetLogo task documentation) of the model.
This modified version is available here.
An optimisation problem 🔗
This model manipulates three parameters:- population: number of Ants in the model,
- evaporation-rate: controls the evaporation rate of the chemical,
- diffusion-rate: controls the diffusion rate of the chemical.
Ants forage from three sources of food (see the number in the picture below). Each source is positioned at different distances from the Ant colony.
 It can be interesting to search for the best combination of the two parameters
It can be interesting to search for the best combination of the two parameters evaporation-rate and diffusion-rate which minimises the eating time of each food source.
To build our fitness function, we modify the NetLogo Ants source code to store, for each food source, the first ticks indicating that this food source is empty.
to compute-fitness
if ((sum [food] of patches with [food-source-number = 1] = 0) and (final-ticks-food1 = 0)) [
set final-ticks-food1 ticks ]
if ((sum [food] of patches with [food-source-number = 2] = 0) and (final-ticks-food2 = 0)) [
set final-ticks-food2 ticks ]
if ((sum [food] of patches with [food-source-number = 3] = 0) and (final-ticks-food3 = 0)) [
set final-ticks-food3 ticks ]
end- The simulation ticks indicating that source 1 is empty,
- The simulation ticks indicating that source 2 is empty,
- The simulation ticks indicating that source 3 is empty.
Run it in OpenMOLE 🔗
When building a calibration or optimisation workflow, the first step is to make the model run in OpenMOLE. This script simply plugs the NetLogo model, and runs one single execution of the model with arbitrary parameters. More details about the NetLogo5 task used in this script can be found in this section of the documentation. // Define the input variables
val gPopulation = Val[Double]
val gDiffusionRate = Val[Double]
val gEvaporationRate = Val[Double]
val mySeed = Val[Int]
// Define the output variables
val food1 = Val[Double]
val food2 = Val[Double]
val food3 = Val[Double]
// Define the NetlogoTask
val ants =
NetLogo5Task(workDirectory / "Ants.nlogo", go = Seq("run-to-grid"), seed = mySeed) set (
// Map the OpenMOLE variables to NetLogo variables
inputs += gPopulation mapped "gpopulation",
inputs += gDiffusionRate mapped "gdiffusion-rate",
inputs += gEvaporationRate mapped "gevaporation-rate",
outputs += food1 mapped "final-ticks-food1",
outputs += food2 mapped "final-ticks-food2",
outputs += food3 mapped "final-ticks-food3",
// Define default values for inputs of the model
mySeed := 42,
gPopulation := 125.0,
gDiffusionRate := 50.0,
gEvaporationRate := 50
)
// Define the hooks to collect the results
val displayHook = DisplayHook(food1, food2, food3)
//Define the environment
val env = LocalEnvironment(5)
// Start a workflow with 1 task
val model_execution = (ants on env hook displayHook)
model_execution
{food1=746.0, food2=1000.0, food3=2109.0}
The optimisation algorithm 🔗
We will try to find the parameter settings minimising these estimators. This script describes how to use the NSGA2 multi-objective optimisation algorithm in OpenMOLE. The result files are written to /tmp/ants.Notice how the
evaluation parameter of the NSGA2Evolution method is the NetLogo task i.e. running the model, which indeed provides an evaluation of the genome (parameter settings) efficiency regarding the objective.
// Define the inputs and their respective variation bounds.
// Define the objectives to minimize.
// Tell OpenMOLE that this model is stochastic and that it should generate a seed for each execution
// Define the fitness evaluation
// Define the parallelism level
// Terminate after 10000 evaluations
// Define a hook to save the Pareto front
NSGA2Evolution(
// Define the inputs and their respective variation bounds.
// Define the objectives to minimize.
genome = Seq(gDiffusionRate in (0.0, 99.0), gEvaporationRate in (0.0, 99.0)),
objective = Seq(food1, food2, food3),
stochastic = Stochastic(seed = mySeed),
evaluation = ants,
parallelism = 10,
termination = 1000
) hook (workDirectory / "results")
Scale up 🔗
If you use distributed computing, it might be a good idea to opt for an island model (see this page) for more details on the island distribution scheme. Islands are better suited to exploit distributed computing resources than classical generational genetic algorithms. See how the end of the script changes to implement islands in the workflow. Here we compute 2,000 islands in parallel, each running during 10 minutes on the European grid:// Define the execution environment
val env = EGIEnvironment("vo.complex-systems.eu")
// Define the island model with 1,000 concurrent islands.
// Each island start from the current state of the algorithm and evolve from there during 10 minutes
// The algorithm stops after 10,000,000 individuals have been evaluated.
NSGA2Evolution(
genome = Seq(gDiffusionRate in (0.0, 99.0), gEvaporationRate in (0.0, 99.0)),
objective = Seq(food1, food2, food3),
stochastic = Stochastic(seed = mySeed),
evaluation = ants,
termination = 10000000,
parallelism = 1000
) by Island(10 minutes) on env hook (workDirectory / "results")